【计算机组成原理】详细解读带符号整数在计算机中的运算

在接下来的内容中，我们将深入探讨原码、反码和补码这三种形式的运算。今天，我们将从最基本的有符号整数运算开始介绍。

之前我们提到过，使用原码进行有符号整数运算时会遇到一些问题：

对于不同符号的加法运算（或同符号的减法运算），需要执行三步运算：比较两个数的绝对值大小，用绝对值较大的数减去绝对值较小的数，为运算结果选择合适的符号。对于同符号的加法运算（或不同符号的减法运算），同样需要执行三步运算：将减法运算转化为加法运算，即加上被减数的相反数，从右到左逐位相加，符号位不参与运算，符号位取左操作数的符号。可以看出，同样是加减法运算，由于操作对象的不同，其运算方式也有所差异。为了提高运算效率，降低硬件开发成本，引入了补码。那么，有符号整数的补码形式是如何进行运算的呢？接下来我们一起来探讨补码的加减运算。

一、补码的优势在原码运算中，由于机器数的最高位表示符号位，且符号位不参与运算，因此实际运算的只有除符号位之外的数值位，而运算结果的符号需要根据结果进行判断，这使得运算过程变得非常复杂。

但在补码运算中，符号位参与运算，我们无需再考虑结果的符号，运算完成后，运算结果的符号自然确定下来，这大大降低了运算的难度。

从这些方面来看，有符号整数以补码形式存储并通过补码运算的优势是显而易见的。

二、补码的加法运算有符号整数的补码加法规则非常简单，从右到左依次相加，逢二进一，如下图所示：

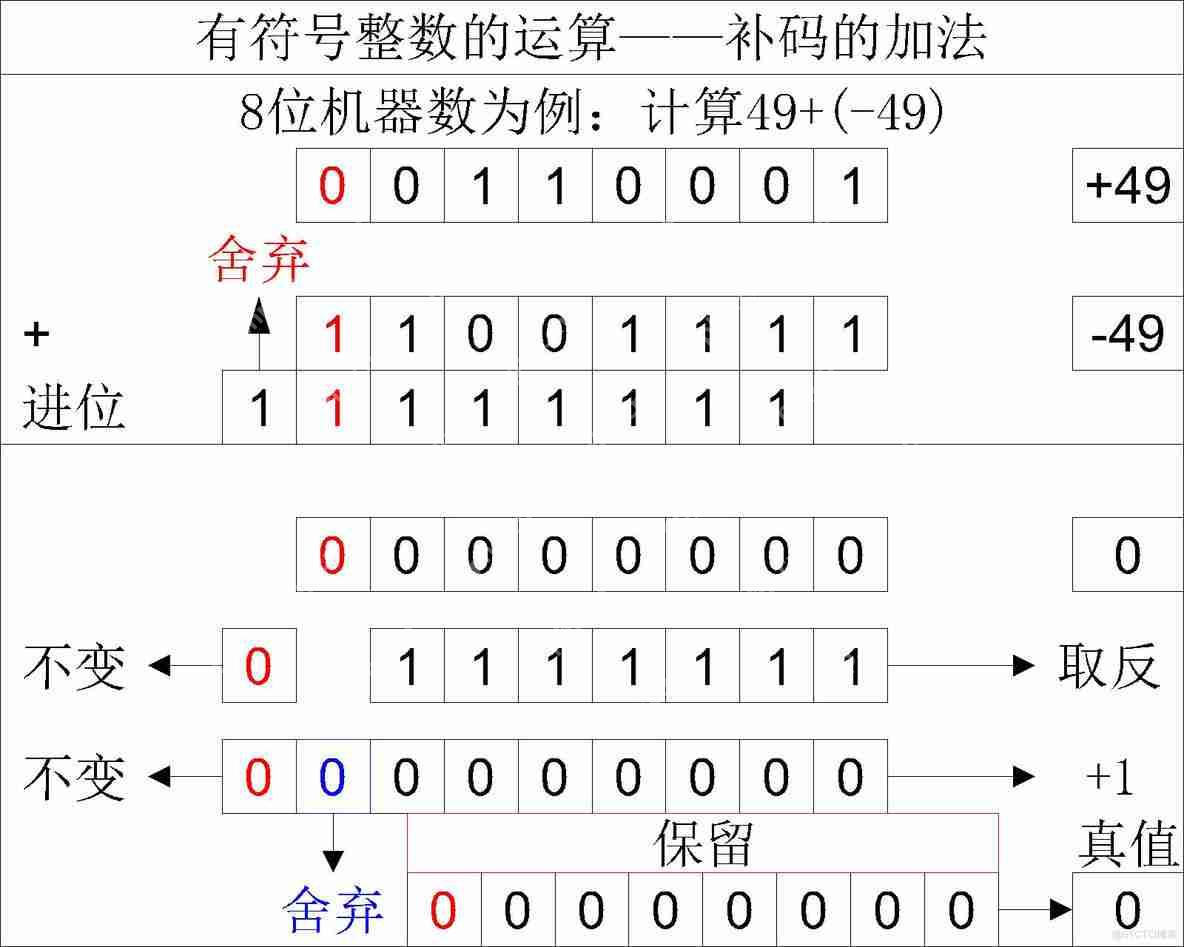可以看到，整个过程并不复杂，细心的朋友会发现，除了后续的补码转换成原码之外，整个加法运算过程与无符号整数的加法运算完全一致。那么，补码的运算是否与无符号整数的运算有关呢？

在无符号整数的运算中，我们已经介绍过，计算机中的减法电路成本高于加法电路成本，因此，为了节约开发成本，计算机中的减法都以加法的形式来完成，这也包括有符号整数的加法。

那么，有符号整数的减法是如何实现的呢？接下来我们继续探讨有符号整数的减法运算。

三、补码的减法运算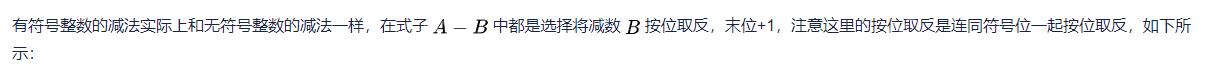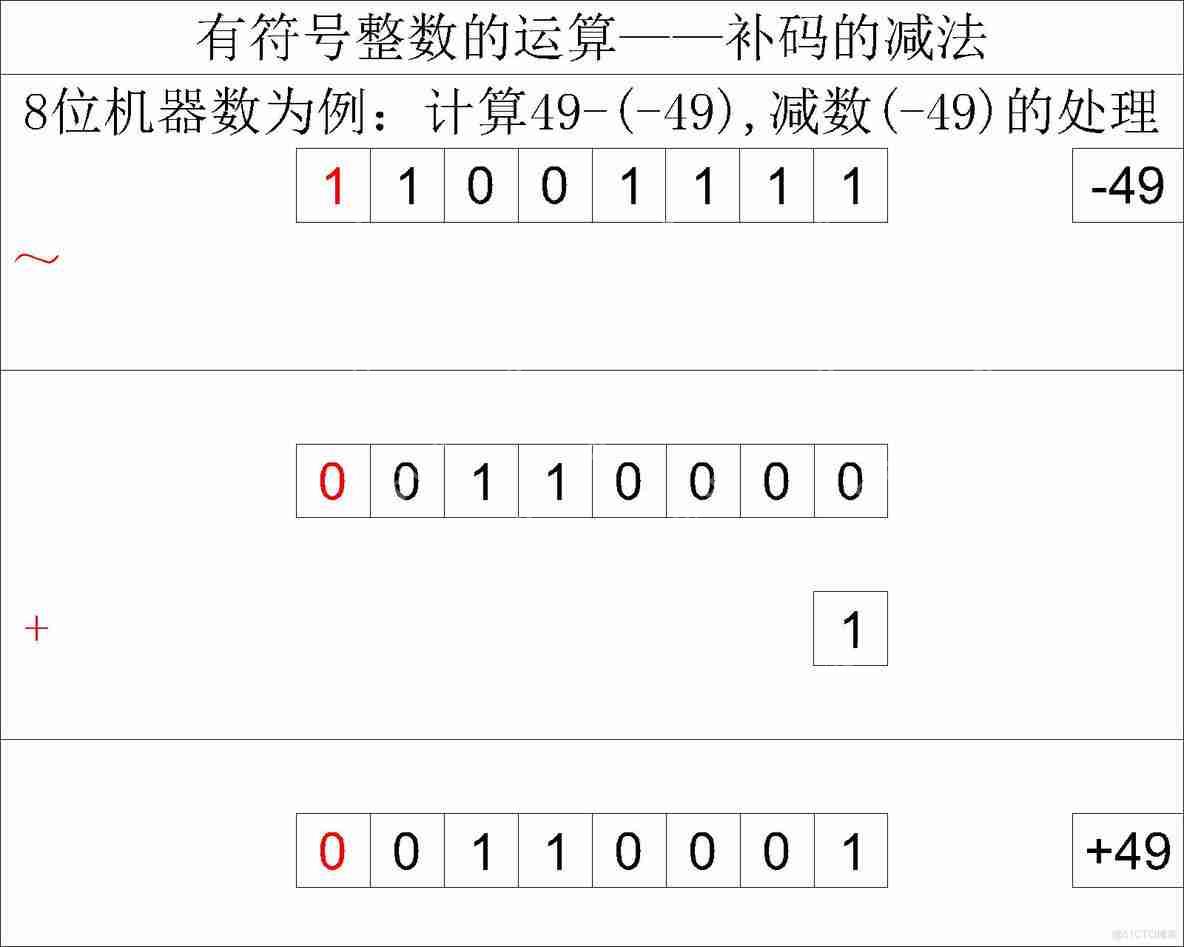完成转换后，我们会发现，最终得到的数值应该是减数的相反数，这是为什么呢？

其实这很好理解，我们需要注意减数的转换步骤：

首先转换数值位：按位取反，末位加1，这一步转换得到的是减数对应的原码。然后转换符号位：按位取反，此时负数变成了正数。经过这一步转换后，得到的是原数的相反数。对于正数的转换过程如下：

首先转换符号位：按位取反，此时整数变成了负数。然后转换数值位：按位取反，末位加1，这一步得到的是负数的补码。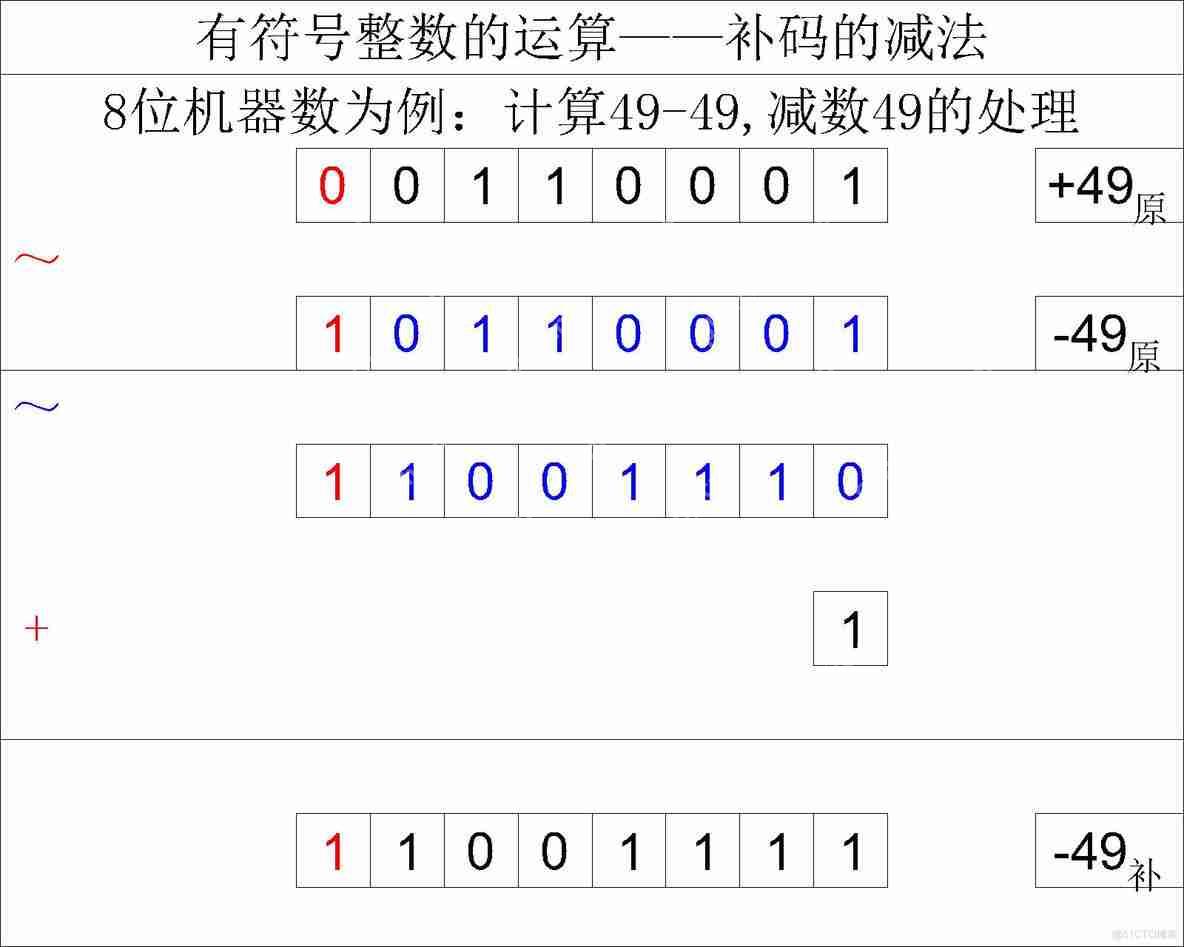从正数的转换来看，更准确的说法应该是获取相反数的补码：

正数：获取的是其对应负数的补码。负数：获取的是其对应正数的补码。完成转换后，减法就变成了加法，其运算规则为：从右到左逐位相加，逢二进一。

现在大家发现了什么吗？

没错，当有符号整数以补码形式进行运算时，其运算过程与无符号整数的运算一致。也就是说，使用补码形式存储有符号整数，可以使用同一个电路来完成无符号整数和有符号整数的运算，而且使用的是成本较低的加法电路。

四、原码、反码、补码的特性接下来我们对原码、反码和补码的特性进行总结，以n位机器数为例，我们将从不同方面进行对比：

真值0的表示形式 运算方式：原码：数值位运算，符号位不参与运算。反码：不参与运算。补码：数值位和符号位都参与运算。无符号整数：所有二进制位都参与运算。结语今天的内容到此结束。在下一篇文章中，我们将介绍《移码》的相关内容，大家记得关注哦！如果大家喜欢博主的文章，可以点赞、收藏并评论支持博主，当然也可以将博主的文章转发给需要的朋友。最后，感谢各位朋友的支持，我们下一篇再见！！！