一种全新的高速乘法算法--mfast【专为MC设计】【BE/JE】
(以下三个图片简单介绍了一下经典乘法算法,这里就不赘述了)乘法,作为四大算数法则之一,一直在数据的处理上占有重要地位,而乘法算法的
(以下三个图片简单介绍了一下经典乘法算法,这里就不赘述了)
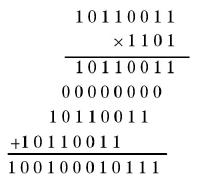
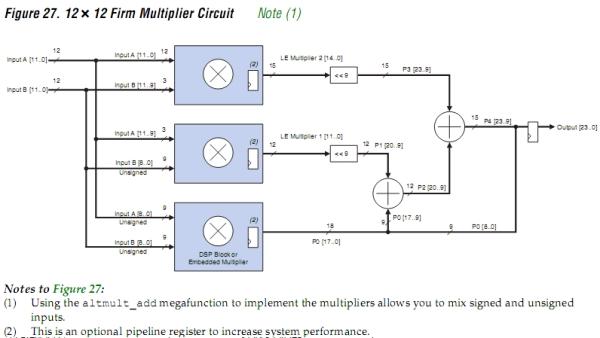
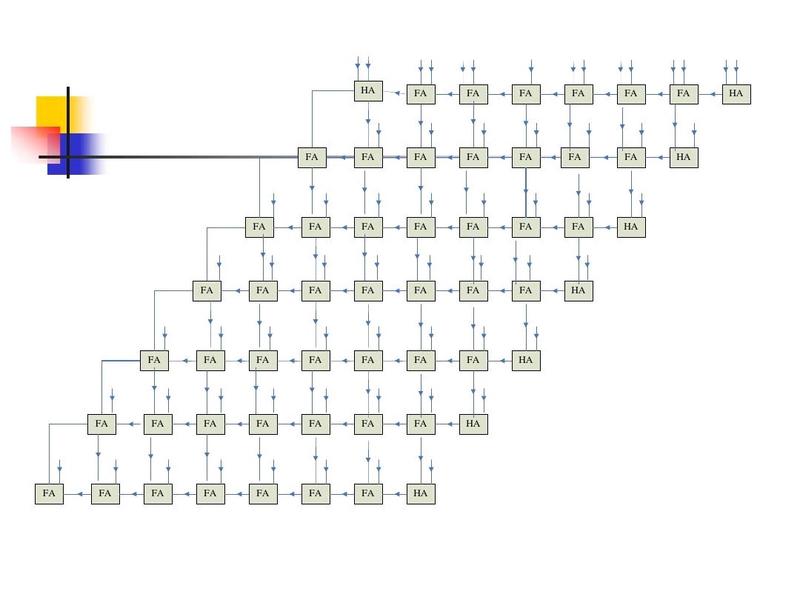
乘法,作为四大算数法则之一,一直在数据的处理上占有重要地位,而乘法算法的有效优化,能使数据的处理效率大幅提升。现在,笔者发现了一种新的硬件乘法优化算法。
在开始之前,我们需要先引入几个概念以做铺垫。首先,乘法有两个乘数,分别设为x和y,我们不妨将y设为能控制电路运行的主乘数。由于y在运行中会经历若干个向右移位,因而必然产生三个会随时间而变化且对过程产生影响的变量。这三个变量一个是最低位所对应的N(now),二是与最低位相邻的那一位所对应的A(above),三是上一个最低位B(below)。这三个变量中,对当前状态影响最大的是A和N,我们不妨设一个二元有序数对
铺垫完成后,我们再来阐述mfast算法的总体结构。该算法分为三大部分,一是全局处理,二是普通处理,三是特殊处理。
对于全局处理,它实际上是一种整体性的结构。我们首先须将一个普通处理单元和一个特殊处理单元编做一个组,组个数视情况而定。多个组在运行时保持独立,达到输出标准后等待求和时钟以便将各个部分积相加。加法部分由一配有恒定时钟和相应电路的CCA充当,用于将从各个部分积生成器中传来的数据逐一相加。待全部运算完成后,由CCA输出。
对于普通处理,它可分为四个状态,这些状态大多在下一时钟到来时才可能发生转移且常常只持续一个周期。这四个状态,依次是LS(左移)状态,R(储存)状态,BCS状态和CCA状态。
当电路启动时,会默认进入LS状态,同时y左移一位并实时监测临界值,启动各个时钟。之后,进入一个可中断的循环。循环是由四种状态案特定顺序排列而成,具体规律由y决定且周期不定长。
LS状态进行的操作,是同时在移位寄存器a中将x左移一位,在移位寄存器c中将y右移一位并实时监测临界值。R状态进行的操作,是将移位寄存器a中的当前值存入移位寄存器b中,同时x,y可继续位移直到临界值为<0,1>。BCS状态,是将x的移位寄存器中的当前值在BCS中减去R中的值并等待CCA时钟以便将结果同步送入CCA。CCA状态,则是将传来的数据在CCA中在同一个时钟上边沿相加。此外,移位寄存器b只会在特殊处理中使用移位功能,其充当通用寄存器使用。
这四个状态发生转移的条件,是在<0,1>或<1,0>或完成时或相邻周期到来时。当临界值为<1,0>时,由LS状态转R状态,在下一周期到来时转回LS状态。当临界值为<0,1>时,由LS状态转至CCA状态,在下一时钟到来时由CCA状态转回LS状态。当完成后,由LS或BCS状态转至CCA状态,不再转回。
对于特殊处理,它是专门针对数据中可能出现的周期性部分而设计的。经分析可知,有三种周期长共8种周期值值得优化,分别为:01;110,101,011;1110,1101,1011,0111。具体算法会在每次y左移一位时同步启动。首先同时检测y的0~3位是否为0101,0~2位是否只有1个0存在,若都不成立则结束。若只存在一个0超前检测一定位数(可为3~4位),若无周期则结束,若有周期且周期长为3或4,则将该片段分段并进行周期式处理。若为0101,则按周期长为2进行分段和周期性处理,反之则结束。
所谓周期性处理,是先用普通处理算出一个周期的值并存入移位寄存器a中,同时将移位寄存器b清零,存入x并进行连续移位至周期结束位。在移位寄存器b移位的同时,移位寄存器a进行连续移位操作并在完成每个周期的移位后输出至CCA(不清零)即可。输出时需等待同步时钟。移位寄存器a完成周期性处理的全部移位后,清零,装入移位寄存器b中值,按普通处理完成后续操作。如果移位寄存器a率先完成周期性处理最后的输出和清零,则等待一段时间直至移位寄存器b完成后再进行装载。
注:若算法重名则为巧合,作者卑微高中生
(欢迎大家来996工程组)(QQ537944302)
(温馨提示,群管理emm比较暴躁)
菜鸟下载发布此文仅为传递信息,不代表菜鸟下载认同其观点或证实其描述。
相关文章
更多>>热门游戏
更多>>热点资讯
更多>>热门排行
更多>>- 神圣王座手游排行榜-神圣王座手游下载-神圣王座游戏版本大全
- 2023末日扳机手游排行榜-末日扳机手游2023排行榜前十名下载
- 一刀屠龙游戏排行-一刀屠龙所有版本-一刀屠龙游戏合集
- 类似凤鸣九州的游戏排行榜_有哪些类似凤鸣九州的游戏
- 类似仙域争霸的游戏排行榜_有哪些类似仙域争霸的游戏
- 九龙霸域手游2023排行榜前十名下载_好玩的九龙霸域手游大全
- 至尊归来手游2023排行榜前十名下载_好玩的至尊归来手游大全
- 多种热门耐玩的九四神途破解版游戏下载排行榜-九四神途破解版下载大全
- 道君问仙手游排行-道君问仙免费版/单机版/破解版-道君问仙版本大全
- 灵域迷失游戏版本排行榜-灵域迷失游戏合集-2023灵域迷失游戏版本推荐
- 部落燃烧游戏排行-部落燃烧所有版本-部落燃烧游戏合集
- 类似仙剑逍遥的游戏排行榜_有哪些类似仙剑逍遥的游戏