基于概率论对明日方舟限定池的数学期望分析
前言 众所周知,限定干员迷迭香的限定池已经结束。我寻访了242次却一次也还没抽到这个限定干员,让我对我的血统产生了深深的怀疑。
前言
众所周知,限定干员迷迭香的限定池已经结束。我寻访了242次却一次也还没抽到这个限定干员,让我对我的血统产生了深深的怀疑。为了更量化地认识到自己的手气,我决定做一个分析。实际上,网络上应该已经有不少卡池概率分析的文献,但我懒得去找,顺带再复习一下概率论。
由于平台编辑器的局限性,对于重要公式,我只能采用图片的形式将其嵌入到文本当中。
摘要
通过概率论,分析明日方舟限定池的概率分布,量化我的欧气值。为了简化模型,本文不考虑前10次保底,以及计算机伪随机数。即考虑理想情况下限定干员的概率分布。
关键字:限定干员、概率
正文
一、数据来源
首先,从官方公告中对限定卡池的描述,我们可以得到一些基础的数据。这些数据将稍后用于整个分析过程。

如上图所示,显然我们可以得到关于六星干员出率的概率。

当然,我们的最终目的是计算限定干员的概率,而下图体现了一部分限定干员出率的概率。
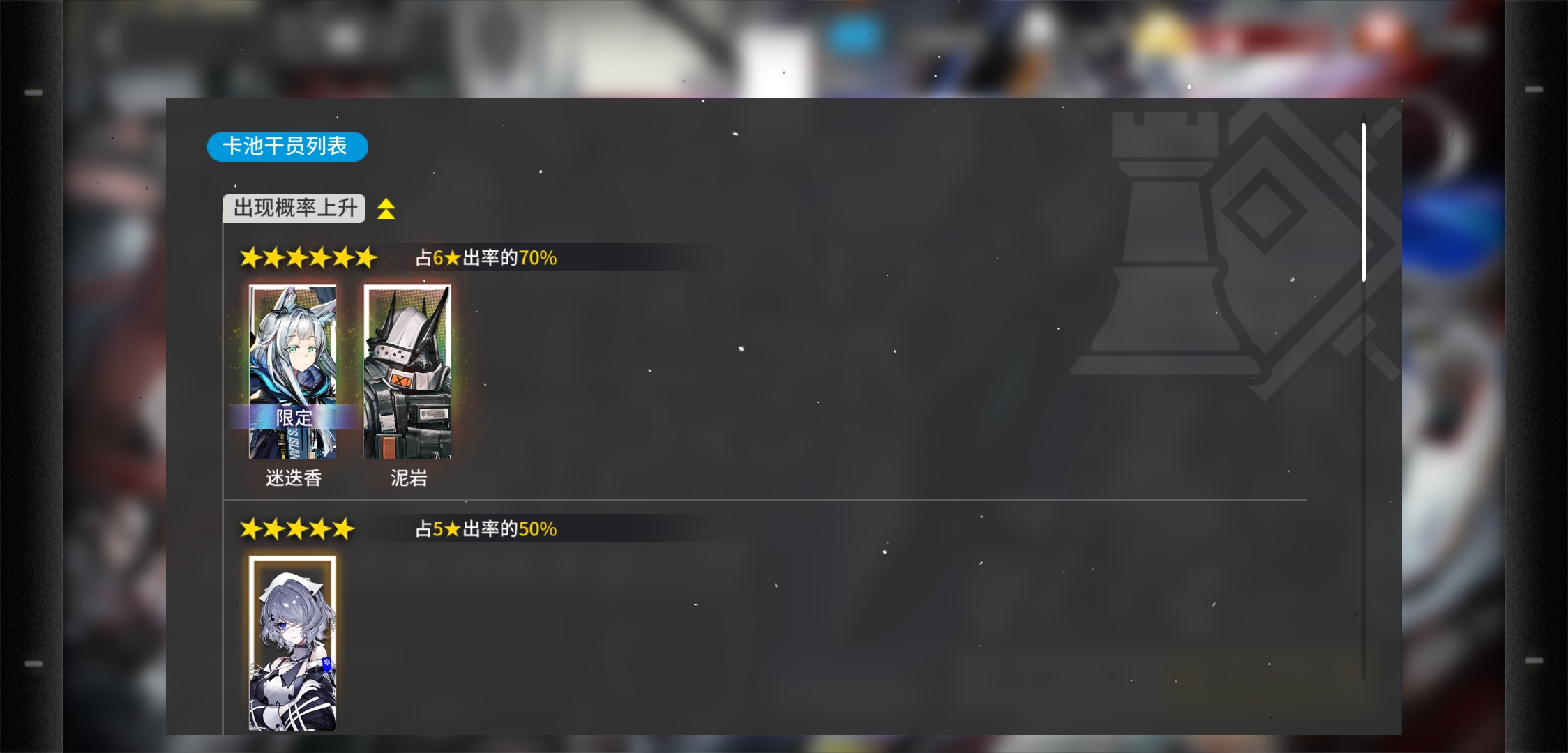
此处,官方并没有直接给出限定干员的出率,而是和另一个UP六星一同描述。设常数a为六星干员中限定干员的出率,显然0 首先考虑抽出一个六星干员的概率分布。设随机变量X表示获得一个六星干员需要寻访的次数。则X的分布律为 当k>50时, 综上所述,X的分布律为 从上式我们可以得出一个结论:当k=56时,概率P{X=k}达到最大值0.0335。数学期望EX=34.59。(计算过程太复杂,我直接用程序跑了) 到目前为止,我们已经得到了获得六星干员的寻访次数概率分布。接下来就是要达到我们的最终目的——获得限定干员的寻访次数概率分布。 获得限定干员,首先要获得一个六星干员,然后才有a的概率是限定干员。但是,在抽到限定干员之前,我们可能会抽到普通的六星干员,使卡池概率重新计算。 设随机变量Y表示获得一个限定干员需要的寻访次数。对于前50项,Y服从超几何分布,即 但当考虑50项以后的概率时,这是一个复杂的情况。因为后面的某一项与之前的事件都不独立。我无法用数学语言给出一个通用的公式,但是我可以用程序语言来描述。 在讲述算法思想之前,我们先看一个k=4时的例子,以便理解随机变量Y与X之间的关系。 当Y=4时,即在第4次抽出限定干员。那么这样的可能性有多少个呢? 每次寻访都出六星,但前3个是非限定,第4个是限定,即a * (1-a)^3 * P{X=1}^4 出了三个六星,那么没出的那一次可能是第1,2,3次,即3 * a * (1-a)^2 * P{X=1}^2 * P{X=2} 出了两个六星,分别抽1,3次,即2 * a * (1-a) * P{X=1} * P{X=3} 出了两个六星,分别抽2,2次,即a * (1-a) * P{X=2}^2 只出一个限定,即a * P{X=4} 不难看出,实际上就是整数拆分,然后乘上对应的系数,最后的累加起来就是最终结果。4的拆分方案还不算多,但如果要算到300的话,以现代电子计算机的能力未必能在人类灭绝之前得出答案。于时我们只能退而求其次,计算一个近似值了。 注意到,随机变量X的概率其实并不大,我们如果取最大值0.034,那么它的7次幂已经是10^(-7)数量级了。那么我们直接把这些次数大的项扔掉就好了。 此外,由于连续不出六星的次数最多是98次,所以在拆分整数时无需考虑大于99的拆分方案。 至此,我们的算法思想就出来了。对于某个整数k,我们使用整数拆分算法将k拆成6个以内的较小数,每个数小于等于99。对于每个拆分方案,计算他们的组合数,也就是这一项的系数。最后进行一个累加结果就出来了。 最后,给出部分的计算结果。这里假设鹰角没有动手脚,常数a取0.35,也就是迷迭香和泥岩对半分。 经过计算我们发现,获得限定干员的最大概率不是k=57,而是氪满300发强娶,概率为9%不到。当然,上表中的数值有一定的误差,一方面是我们把一些项给省略了,另一方面是计算机浮点数精度有限。 什么嘛,原来是242发不出限定只有十分之一的概率,那我也不是很非嘛(
菜鸟下载发布此文仅为传递信息,不代表菜鸟下载认同其观点或证实其描述。
二、开始推导
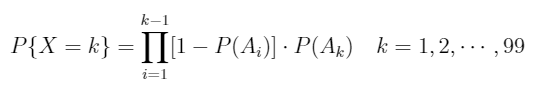

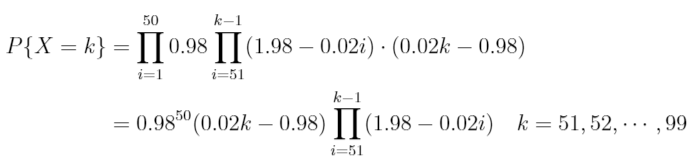
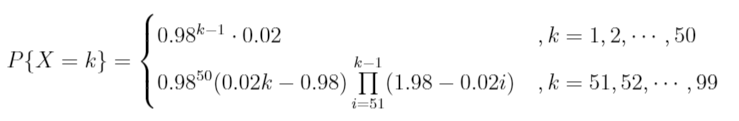

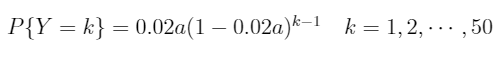
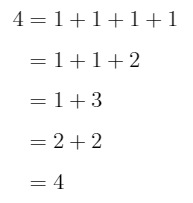



总结
相关文章
更多>>热门游戏
更多>>热点资讯
更多>>热门排行
更多>>- 古仙情缘手游排行榜-古仙情缘手游下载-古仙情缘游戏版本大全
- 奇迹mu系列版本排行-奇迹mu系列游戏有哪些版本-奇迹mu系列游戏破解版
- 姬神物语题材手游排行榜下载-有哪些好玩的姬神物语题材手机游戏推荐
- 莽荒天下手游排行-莽荒天下免费版/单机版/破解版-莽荒天下版本大全
- 一念江湖游戏排行-一念江湖所有版本-一念江湖游戏合集
- 九百打金手游2023排行榜前十名下载_好玩的九百打金手游大全
- 守护者们游戏排行-守护者们所有版本-守护者们游戏合集
- 地藏系列版本排行-地藏系列游戏有哪些版本-地藏系列游戏破解版
- 2023火线精英手游排行榜-火线精英手游2023排行榜前十名下载
- 多种热门耐玩的戮神传奇破解版游戏下载排行榜-戮神传奇破解版下载大全
- 群星守卫系列版本排行-群星守卫系列游戏有哪些版本-群星守卫系列游戏破解版
- 2023次元幻境手游排行榜-次元幻境手游2023排行榜前十名下载